循环冗余校验码CRC

简介

循环冗余校验（英语：Cyclic redundancy check，简写“CRC”）是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。生成的数字在传输或者存储之前计算出来并且附加到数据后面，然后接收方进行检验确定数据是否发生变化。一般来说，循环冗余校验的值都是32位的整数。由于本函数易于用二进制的计算机硬件使用、容易进行数学分析并且尤其善于检测传输通道干扰引起的错误，因此获得广泛应用。此方法是由W. Wesley Peterson于1961年发表

步骤

1. 发送端与接收端事先商定一个 生成多项式 $G(x)$，并将其转换为二进制表达式
2. 将$n$位原始数据左移 $k$ 位，形成$n+k$位的信息码 $M(x)$
3. $M(x)$模2除$G(x)$，得到商$Q(x)$和余数$R(x)$，其中余数即为CRC码
4. 将求得的CRC码附加到原始数据后面，发送给接收端
5. 接收端收到数据后模2除$G(x)$，若能整除表示正确，不能则说明有错误

   注解

   • 生成多项式$G(x)$：
     生成多项式有国际标准选择，但最高位和最低位必须均为“1”
     不是任何一个多项式都能用作生成多项式。要能进行检错和纠错就应满足
     （1）任何一位出错，余数都不应为0；
     （2）不同位出错，余数应不同；
     （3）对余数继续进行模2运算，应使余数循环。
   • 左移$k$位：左移的位数取决于生成多项式$G(x)$的最高次幂$k$
   • 模2除：运算时不考虑进位和借位，即为XOR运算
   • 余数$R(x)$：余数的位数等于最高次幂$k$，不足时余数前面的0不能省略

例

Q：要发送的二进制数据为1100，设生成多项式$G(x)=x^3+x+1$，求CRC码。
A：

1. 生成多项式的最高次幂为3，二进制表达为1011
2. 1100左移3位，即为1100000
3. 计算如图
   
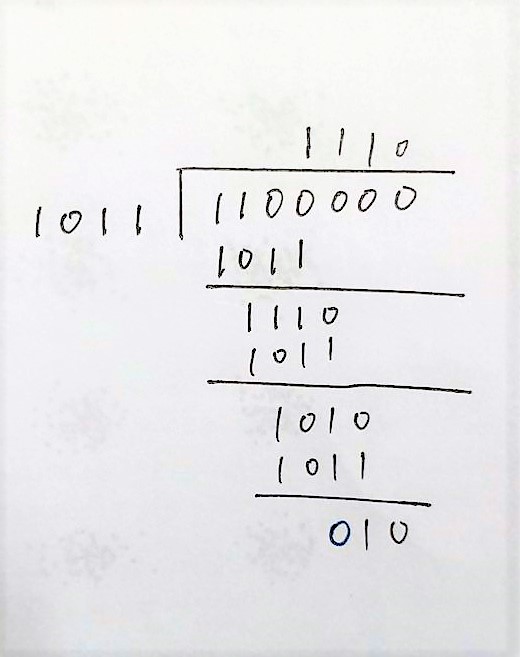
4. 得到余数为010，即为所求。发送的数据为1100010

ref

• 计算机组成原理教程
• 循环冗余校验